Recursive least squares filter
The Recursive least squares (RLS) adaptive filter is an algorithm which recursively finds the filter coefficients that minimize a weighted linear least squares cost function relating to the input signals. This is in contrast to other algorithms such as the least mean squares (LMS) that aim to reduce the mean square error. In the derivation of the RLS, the input signals are considered deterministic, while for the LMS and similar algorithm they are considered stochastic. Compared to most of its competitors, the RLS exhibits extremely fast convergence. However, this benefit comes at the cost of high computational complexity,
Contents |
Motivation
In general, the RLS can be used to solve any problem that can be solved by adaptive filters. For example, suppose that a signal d(n) is transmitted over an echoey, noisy channel that causes it to be received as
where 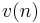 represents additive noise. We will attempt to recover the desired signal
represents additive noise. We will attempt to recover the desired signal 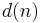 by use of a
by use of a 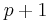 -tap FIR filter,
-tap FIR filter, 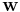 :
:
where ![\mathbf{x}_n=[x(n)\quad x(n-1)\quad\ldots\quad x(n-p)]^T](/2012-wikipedia_en_all_nopic_01_2012/I/6e0d92acb39995004e6a6a0fcedf83a8.png) is the vector containing the
is the vector containing the  most recent samples of
most recent samples of 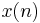 . Our goal is to estimate the parameters of the filter
. Our goal is to estimate the parameters of the filter 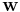 , and at each time n we refer to the new least squares estimate by
, and at each time n we refer to the new least squares estimate by 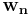 . As time evolves, we would like to avoid completely redoing the least squares algorithm to find the new estimate for
. As time evolves, we would like to avoid completely redoing the least squares algorithm to find the new estimate for 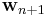 , in terms of
, in terms of 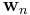 .
.
The benefit of the RLS algorithm is that there is no need to invert matrices, thereby saving computational power. Another advantage is that it provides intuition behind such results as the Kalman filter.
Discussion
The idea behind RLS filters is to minimize a cost function  by appropriately selecting the filter coefficients
by appropriately selecting the filter coefficients 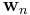 , updating the filter as new data arrives. The error signal
, updating the filter as new data arrives. The error signal 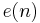 and desired signal
and desired signal 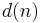 are defined in the negative feedback diagram below:
are defined in the negative feedback diagram below:
The error implicitly depends on the filter coefficients through the estimate 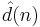 :
:
The weighted least squares error function  —the cost function we desire to minimize—being a function of e(n) is therefore also dependent on the filter coefficients:
—the cost function we desire to minimize—being a function of e(n) is therefore also dependent on the filter coefficients:
where 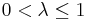 is the "forgetting factor" which gives exponentially less weight to older error samples.
is the "forgetting factor" which gives exponentially less weight to older error samples.
The cost function is minimized by taking the partial derivatives for all entries  of the coefficient vector
of the coefficient vector 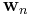 and setting the results to zero
and setting the results to zero
Next, replace 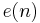 with the definition of the error signal
with the definition of the error signal
Rearranging the equation yields
This form can be expressed in terms of matrices
where 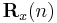 is the weighted sample correlation matrix for
is the weighted sample correlation matrix for 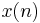 , and
, and 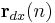 is the equivalent estimate for the cross-correlation between
is the equivalent estimate for the cross-correlation between 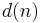 and
and 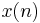 . Based on this expression we find the coefficients which minimize the cost function as
. Based on this expression we find the coefficients which minimize the cost function as
This is the main result of the discussion.
Choosing 
The smaller  is, the smaller contribution of previous samples. This makes the filter more sensitive to recent samples, which means more fluctuations in the filter co-efficients. The
is, the smaller contribution of previous samples. This makes the filter more sensitive to recent samples, which means more fluctuations in the filter co-efficients. The 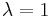 case is referred to as the growing window RLS algorithm.
case is referred to as the growing window RLS algorithm.
Recursive algorithm
The discussion resulted in a single equation to determine a coefficient vector which minimizes the cost function. In this section we want to derive a recursive solution of the form
where 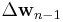 is a correction factor at time
is a correction factor at time 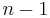 . We start the derivation of the recursive algorithm by expressing the cross correlation
. We start the derivation of the recursive algorithm by expressing the cross correlation 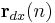 in terms of
in terms of 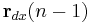
where 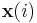 is the
is the 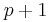 dimensional data vector
dimensional data vector
Similarly we express 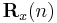 in terms of
in terms of 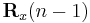 by
by
In order to generate the coefficient vector we are interested in the inverse of the deterministic autocorrelation matrix. For that task the Woodbury matrix identity comes in handy. With
-

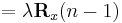 is
is 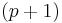 -by-
-by-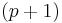

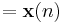 is
is 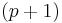 -by-1
-by-1
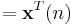 is 1-by-
is 1-by-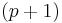

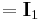 is the 1-by-1 identity matrix
is the 1-by-1 identity matrix
The Woodbury matrix identity follows
To come in line with the standard literature, we define
where the gain vector 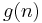 is
is
Before we move on, it is necessary to bring 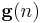 into another form
into another form
Subtracting the second term on the left side yields
With the recursive definition of 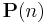 the desired form follows
the desired form follows
Now we are ready to complete the recursion. As discussed
The second step follows from the recursive definition of 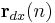 . Next we incorporate the recursive definition of
. Next we incorporate the recursive definition of 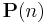 together with the alternate form of
together with the alternate form of 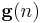 and get
and get
With 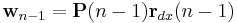 we arrive at the update equation
we arrive at the update equation
where 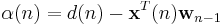 is the a priori error. Compare this with the a posteriori error; the error calculated after the filter is updated:
is the a priori error. Compare this with the a posteriori error; the error calculated after the filter is updated:
That means we found the correction factor
This intuitively satisfying result indicates that the correction factor is directly proportional to both the error and the gain vector, which controls how much sensitivity is desired, through the weighting factor,  .
.
RLS algorithm summary
The RLS algorithm for a p-th order RLS filter can be summarized as
| Parameters: | 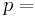 filter order filter order |
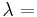 forgetting factor forgetting factor |
|
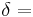 value to initialize value to initialize 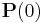 |
|
| Initialization: | 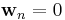 , , |
 , , |
|
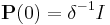 where where  is the identity matrix of rank is the identity matrix of rank 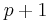 |
|
| Computation: | For 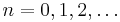 |
|
|
|
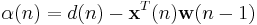 |
|
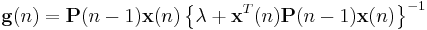 |
|
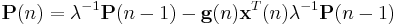 |
|
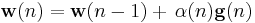 . . |
Note that the recursion for  follows a Riccati equation and thus draws parallels to the Kalman filter.[1]
follows a Riccati equation and thus draws parallels to the Kalman filter.[1]
Lattice recursive least squares filter (LRLS)
The Lattice Recursive Least Squares adaptive filter is related to the standard RLS except that it requires fewer arithmetic operations (order N). It offers additional advantages over conventional LMS algorithms such as faster convergence rates, modular structure, and insensitivity to variations in eigenvalue spread of the input correlation matrix. The LRLS algorithm described is based on a posteriori errors and includes the normalized form. The derivation is similar to the standard RLS algorithm and is based on the definition of 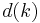 . In the forward prediction case, we have
. In the forward prediction case, we have  with the input signal
with the input signal 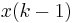 as the most up to date sample. The backward prediction case is
as the most up to date sample. The backward prediction case is 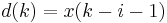 , where i is the index of the sample in the past we want to predict, and the input signal
, where i is the index of the sample in the past we want to predict, and the input signal 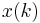 is the most recent sample.[2]
is the most recent sample.[2]
Parameter Summary
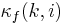 is the forward reflection coefficient
is the forward reflection coefficient
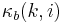 is the backward reflection coefficient
is the backward reflection coefficient
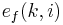 represents the instantaneous a posteriori forward prediction error
represents the instantaneous a posteriori forward prediction error
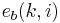 represents the instantaneous a posteriori backward prediction error
represents the instantaneous a posteriori backward prediction error
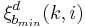 is the minimum least-squares backward prediction error
is the minimum least-squares backward prediction error
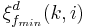 is the minimum least-squares forward prediction error
is the minimum least-squares forward prediction error
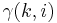 is a conversion factor between a priori and a posteriori errors
is a conversion factor between a priori and a posteriori errors
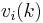 are the feedforward multiplier coefficients.
are the feedforward multiplier coefficients.
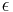 is a small positive constant that can be 0.01
is a small positive constant that can be 0.01
LRLS Algorithm Summary
The algorithm for a LRLS filter can be summarized as
| Initialization: | |
| For i = 0,1,...,N | |
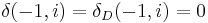 (if x(k) = 0 for k < 0) (if x(k) = 0 for k < 0) |
|
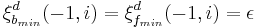 |
|
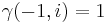 |
|
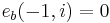 |
|
| End | |
| Computation: | |
| For k ≥ 0 | |
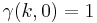 |
|
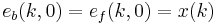 |
|
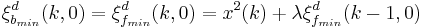 |
|
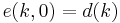 |
|
| For i = 0,1,...,N | |
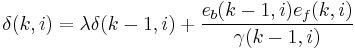 |
|
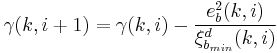 |
|
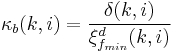 |
|
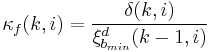 |
|
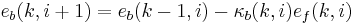 |
|
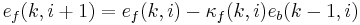 |
|
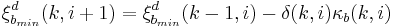 |
|
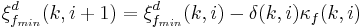 |
|
| Feedforward Filtering | |
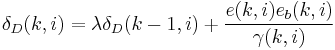 |
|
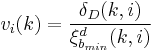 |
|
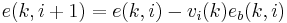 |
|
| End | |
| End | |
Normalized lattice recursive least squares filter (NLRLS)
The normalized form of the LRLS has fewer recursions and variables. It can be calculated by applying a normalization to the internal variables of the algorithm which will keep their magnitude bounded by one. This is generally not used in real-time applications because of the number of division and square-root operations which comes with a high computational load.
NLRLS algorithm summary
The algorithm for a NLRLS filter can be summarized as
| Initialization: | |
| For i = 0,1,...,N | |
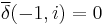 (if x(k) = d(k) = 0 for k < 0) (if x(k) = d(k) = 0 for k < 0) |
|
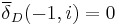 |
|
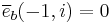 |
|
| End | |
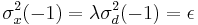 |
|
| Computation: | |
| For k ≥ 0 | |
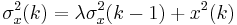 (Input signal energy) (Input signal energy) |
|
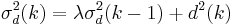 (Reference signal energy) (Reference signal energy) |
|
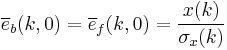 |
|
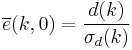 |
|
| For i = 0,1,...,N | |
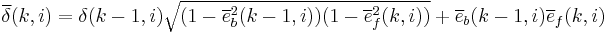 |
|
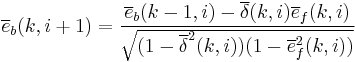 |
|
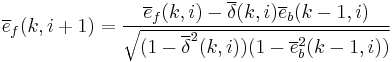 |
|
| Feedforward Filter | |
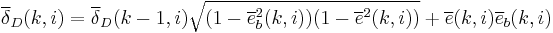 |
|
![\overline{e}(k,i%2B1) = \frac{1}{\sqrt{(1 - \overline{e}_b^2(k,i))(1 - \overline{\delta}_D^2(k,i))}}[\overline{e}(k,i) - \overline{\delta}_D(k,i)\overline{e}_b(k,i)]](/2012-wikipedia_en_all_nopic_01_2012/I/fdebb3bc009fd1d6fb4ef6276a67a581.png) |
|
| End | |
| End | |
See also
- Adaptive filter
- Kernel adaptive filter
- Least mean squares filter
- Real-Time Outbreak and Disease Surveillance (RODS)
References
- Hayes, Monson H. (1996). "9.4: Recursive Least Squares". Statistical Digital Signal Processing and Modeling. Wiley. p. 541. ISBN 0-471-59431-8.
- Simon Haykin, Adaptive Filter Theory, Prentice Hall, 2002, ISBN 0-13-048434-2
- M.H.A Davis, R.B. Vinter, Stochastic Modelling and Control, Springer, 1985, ISBN 0-412-16200-8
- Weifeng Liu, Jose Principe and Simon Haykin, Kernel Adaptive Filtering: A Comprehensive Introduction, John Wiley, 2010, ISBN 0470447532
Notes
- ^ Welch, Greg and Bishop, Gary "An Introduction to the Kalman Filter", Department of Computer Science, University of North Carolina at Chapel Hill, September 17, 1997, accessed July 19, 2011.
- ^ Albu, Kadlec, Softley, Matousek, Hermanek, Coleman, Fagan "Implementation of (Normalised) RLS Lattice on Virtex", Digital Signal Processing, 2001, accessed December 24, 2011.
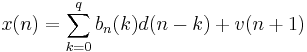
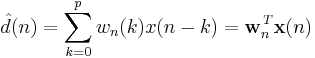
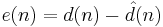
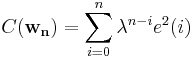
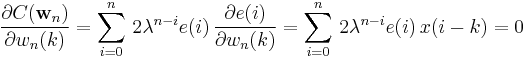
![\sum_{i=0}^{n}\lambda^{n-i}\left[d(i)-\sum_{l=0}^{p}w_{n}(l)x(i-l)\right]x(i-k)= 0](/2012-wikipedia_en_all_nopic_01_2012/I/b0805f4d9e41982827a173cb355658b3.png)
![\sum_{l=0}^{p}w_{n}(l)\left[\sum_{i=0}^{n}\lambda^{n-i}\,x(i-l)x(i-k)\right]= \sum_{i=0}^{n}\lambda^{n-i}d(i)x(i-k)](/2012-wikipedia_en_all_nopic_01_2012/I/fdcb9691c67df2278ffefc7af5d14d3d.png)
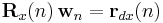
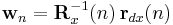
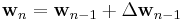
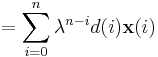
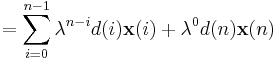
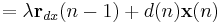
![\mathbf{x}(i)=[x(i), x(i-1), \dots , x(i-p) ]^{T}](/2012-wikipedia_en_all_nopic_01_2012/I/88f689398403f90be9150d809b434a89.png)
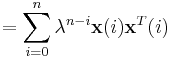
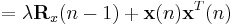
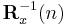

![\left[\lambda\mathbf{R}_{x}(n-1)%2B\mathbf{x}(n)\mathbf{x}^{T}(n)\right]^{-1}](/2012-wikipedia_en_all_nopic_01_2012/I/81b912a627a9ccec69d187bc77fe2568.png)
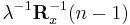
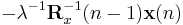
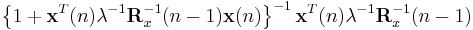
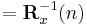
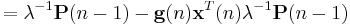
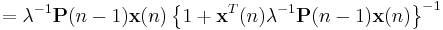
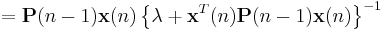
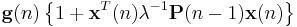
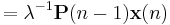
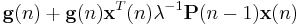
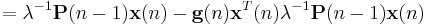
![=\lambda^{-1}\left[\mathbf{P}(n-1)-\mathbf{g}(n)\mathbf{x}^{T}(n)\mathbf{P}(n-1)\right]\mathbf{x}(n)](/2012-wikipedia_en_all_nopic_01_2012/I/8e2f8f0aae42c4dfa8a51433e753acf5.png)
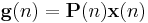
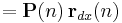
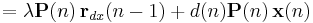
![=\lambda\left[\lambda^{-1}\mathbf{P}(n-1)-\mathbf{g}(n)\mathbf{x}^{T}(n)\lambda^{-1}\mathbf{P}(n-1)\right]\mathbf{r}_{dx}(n-1)%2Bd(n)\mathbf{g}(n)](/2012-wikipedia_en_all_nopic_01_2012/I/15a10952b81b9b184430a87055774af5.png)
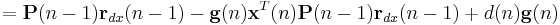
![=\mathbf{P}(n-1)\mathbf{r}_{dx}(n-1)%2B\mathbf{g}(n)\left[d(n)-\mathbf{x}^{T}(n)\mathbf{P}(n-1)\mathbf{r}_{dx}(n-1)\right]](/2012-wikipedia_en_all_nopic_01_2012/I/260c532b5b5f10e0aaacf91e275daffb.png)
![=\mathbf{w}_{n-1}%2B\mathbf{g}(n)\left[d(n)-\mathbf{x}^{T}(n)\mathbf{w}_{n-1}\right]](/2012-wikipedia_en_all_nopic_01_2012/I/39d7735b6d2ba9aaaf944e187522c9a0.png)
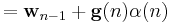
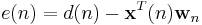
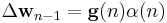
![\mathbf{x}(n) =
\left[
\begin{matrix}
x(n)\\
x(n-1)\\
\vdots\\
x(n-p)
\end{matrix}
\right]](/2012-wikipedia_en_all_nopic_01_2012/I/1ab05ea239b93ac0cde866b244c8574d.png)